Voronoi-Diagramme: Verbirgt sich eine geheime mathematische Ordnung hinter dem Chaos der Natur?
Ein Voronoi-Diagramm ist ein spezielles mathematisches Konzept, das bei der Flächen- und Raumaufteilung hilft. Mit ihm lassen sich etliche Strukturen der Natur erklären und zahlreiche Anwendungen in Wissenschaft und Technik umsetzen.

Das klassische Voronoi-Muster kennt man aus der Natur: Das Fell von Giraffen etwa, das Muster von zerbrochener Keramik oder die Adern in einem Blatt folgen alle demselben Prinzip. In der Mathematik können solche Strukturen mithilfe von Voronoi-Diagrammen beschrieben werden.
In einem Voronoi-Diagramm wird eine Fläche anhand von Punkten, sogenannten Seeds, in Regionen oder Voronoi-Zellen zerlegt, die wiederum durch Voronoi-Kanten voneinander getrennt werden. Ziel des Voronoi-Diagramms ist eine effiziente und vollständige Ausnutzung der gesamten Fläche.
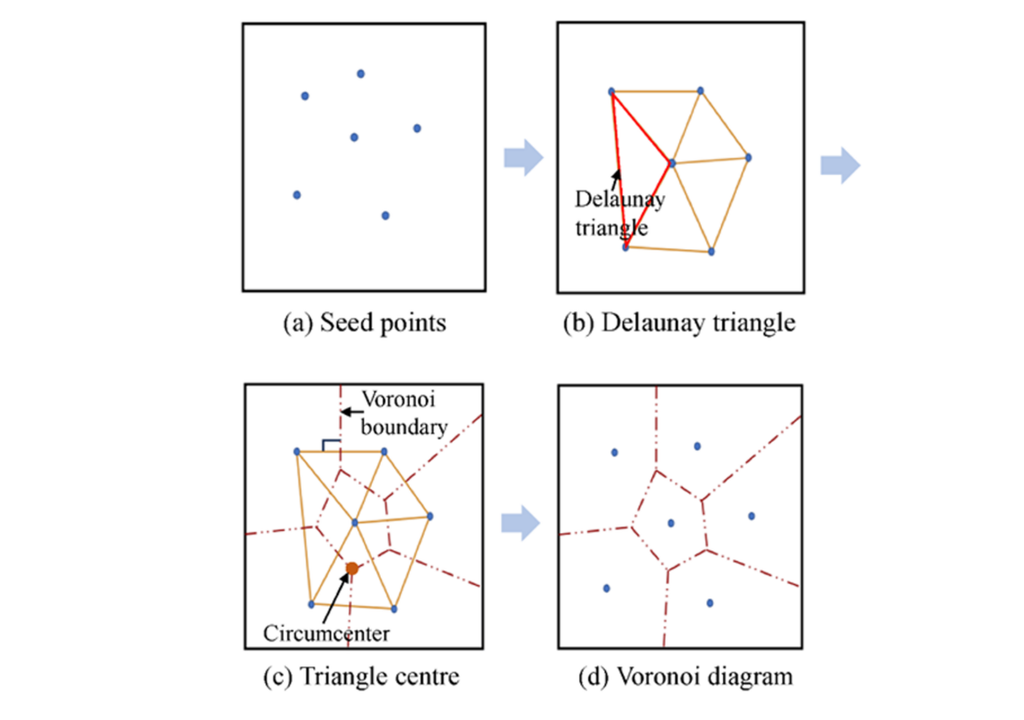
Voronoi-Diagramme haben spezielle mathematische Eigenschaften, beispielsweise liegen Voronoi-Kanten genau mittig und immer senkrecht auf den Verbindungslinien zweier Seeds. Liegen die Seeds in einer euklidischen Ebene, sind die Voronoi-Zellen zudem konvex, das heißt, nach außen gebogen. Es gibt keine Ausbuchtungen innerhalb der einzelnen Zellform.
Voronoi-Diagramme hängen zudem mit einem anderen Konzept zusammen, mit der Delaunay-Triangulation (von engl. triangle = Dreieck). Bei der Delaunay-Triangulation werden nur die Seeds miteinander verbunden, sodass lediglich Dreiecksflächen entstehen. Voronoi-Diagramme und Delaunay-Triangulation kommen beispielsweise in der Geographie zum Einsatz.
Auch darüber hinaus gibt es zahlreiche Beispiele von Voronoi-Mustern, sowohl in der Natur als auch in Wissenschaft und Technik: Als mathematisches Konzept werden die Diagramme vor allem in der Biologie, sowie in Robotik, Telekommunikation, Stadtplanung und Meteorologie verwendet.
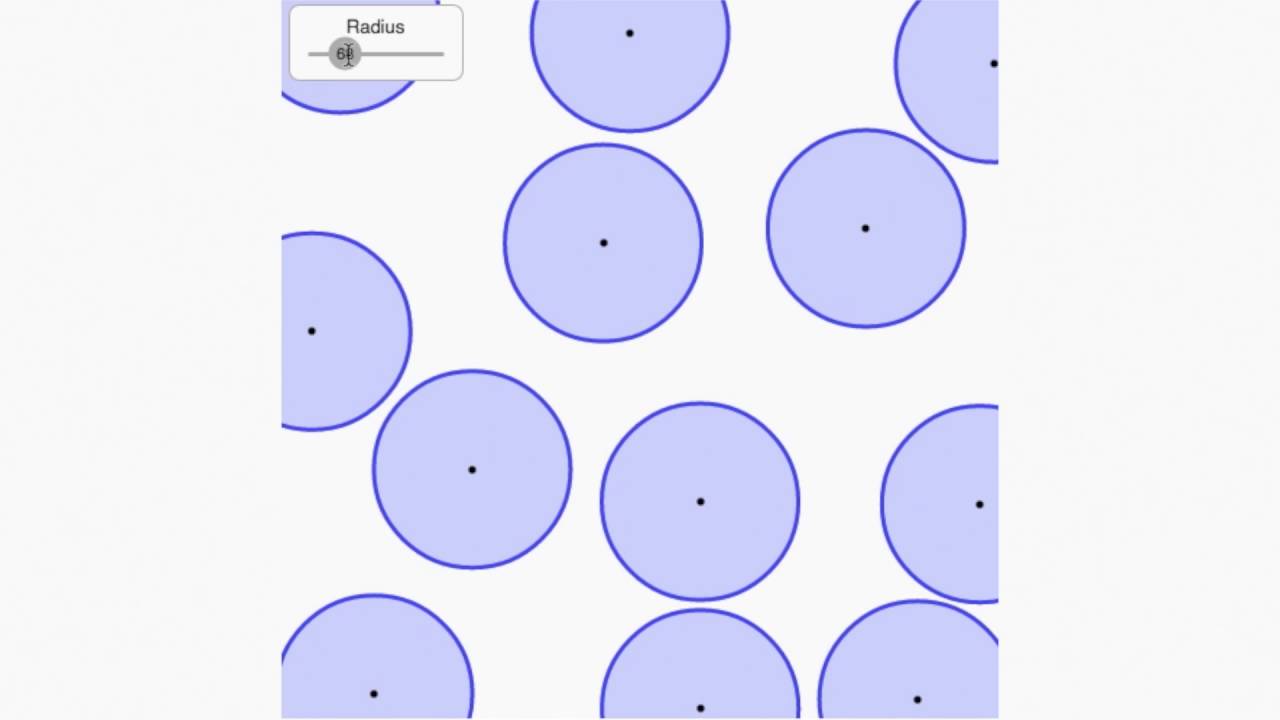
Ein möglicher Ansatz zur Erzeugung von Voronoi-Diagrammen besteht darin, für jeden Punkt den nächstgelegenen Seed zu bestimmen und diesen Punkt einer neuen Voronoi-Zelle zuzuweisen. Für große Datensätze ist ein solcher Ansatz jedoch wegen der Zeitkomplexität zu ineffizient. Daher sind für umfangreiche Datenmengen spezielle Algorithmen vonnöten, wie etwa der Fortune-Algorithmus.
In der Natur ...
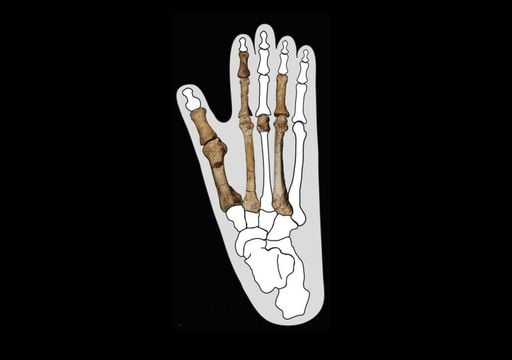
Natürliche Voronoi-Strukturen sind beispielsweise Tier- und Pflanzenzellen sowie die Struktur von Knochenzellen. Das Fellmuster von Giraffen und die Schuppen von Schlangen folgen ebenfalls einem Voronoi-Muster. Schaum mit Seifenblasen entspricht ebenso dem Verteilungsprinzip.
Außerdem zählen Austrocknungsmuster und Risse, etwa bei Keramik oder trockener Erde, sowie Maiskörner, Libellenflügel und Blattadern zu den klassischen Voronoi-Beispielen – und die Liste ließe sich beliebig fortsetzen. Für die Wissenschaft bietet die mathematische Beschreibung nach Voronoi die Möglichkeit, das Kristall- oder Korallenwachstum zu beschreiben oder die Tierverteilung anhand von Revieren zu verstehen.

Die gewonnenen Erkenntnisse können darüber hinaus auch im Bereich Bionik angewendet werden, beispielsweise in der Medizin bei Knochenimplantaten oder bei Hörgeräten und Cochlea-Implantaten. Insbesondere zur Materialeinsparung – etwa beim Brückenbau oder bei der Herstellung von Prothesen – können Voronoi-Strukturen Anwendung finden.
... sowie in Wissenschaft und Technik
Zum Beispiel können Voronoi-Diagramme in der Stadtplanung dazu verwendet werden, städtische Versorgungsbereiche zu untersuchen, etwa Einzugsgebiete von Krankenhäusern. In der Biologie werden Voronoi-Diagramme hingegen zur Modellierung von Zellstrukturen verwendet: Zellen organisieren sich in Geweben derart, dass sie den Raum effizient ausfüllen, daher können Voronoi-Diagramme die Zellverteilung analysieren und simulieren.
In der Robotik helfen Voronoi-Diagramme bei der Navigation und Pfadplanung. So können etwa Multi-Roboter-Systeme bei der Abdeckung einer Region unterstützen, indem sie beispielsweise Ressourcen in Meeresgebieten auskundschaften, Pestizide und Düngemittel über landwirtschaftliche Flächen sprühen und bei Such- und Rettungsmissionen in Katastrophengebieten aus der Luft helfen.
Auch bei der Positionierung von Mobilfunkmasten, also im Bereich der Netzabdeckung, kommen entsprechende Berechnungen zum Einsatz, ebenso bei der Analyse von Wetterdaten und der Ermittlung von Niederschlagsverteilungen.
Voronoi-Diagramme können bei der Lösung komplexer mathematischer Probleme helfen und sind ein leistungsstarkes Werkzeug zur Analyse und Visualisierung räumlicher Daten. Dadurch, dass sie Flächen logisch und effizient unterteilen, sind sie in vielen Disziplinen eine hilfreiche Berechnungsmethode.
---
Quellen:
Liu Q, Zhao X, Duan Y, Qin M, Xie W, Sun W. (2024): Dynamic Construction of Spherical Raster Voronoi Diagrams Based on Ordered Dilation. ISPRS International Journal of Geo-Information, 13(6), 202. https://doi.org/10.3390/ijgi13060202
Zhou, M., Li, J., Wang, C., Wang, J., & Wang, L. (2024): Applications of Voronoi Diagrams in Multi-Robot Coverage: A Review. Journal of Marine Science and Engineering, 12(6), 1022. https://doi.org/10.3390/jmse12061022