Kann man sagen, dass es in der Mathematik schöne Gleichungen gibt? Die Wissenschaftler sagen ja
Laut Mathematikern sind die schönsten, anspruchsvollsten und überzeugendsten Gleichungen aufgedeckt worden - einige davon finden Sie hier!
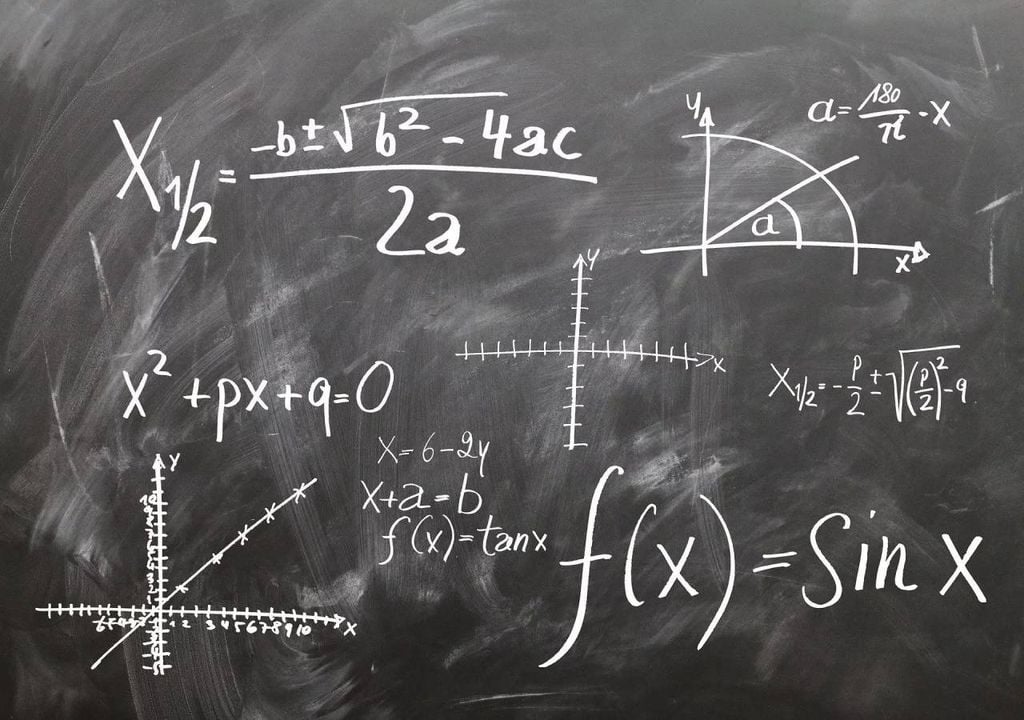
Mathematiker betrachten Gleichungen als Kunst. Genauso wie viele von einem Gemälde oder einem Musikstück bewegt werden, können für diejenigen, die Mathematik schätzen und verstehen, Ausdrücke von Zahlen, Variablen, Operationen und Beziehungen zwischen Mengen ebenso ansprechend sein.
Wie bei der künstlerischen Schönheit liegt die mathematische Schönheit im Auge des Betrachters", und ein Mathematiker mag einfache und prägnante Gleichungen schätzen, während ein anderer das Gegenteil bevorzugt.
So werden sowohl antike als auch moderne Gleichungen für ihre Intelligenz, Kraft und Fähigkeit bewundert.
Loewner Differentialgleichung
Die Loewner-Differentialgleichung wurde 1923 von Charles Loewner eingeführt und beschreibt die zeitliche Entwicklung einer Familie von konformen Funktionen (winkelerhaltend), die auf Teilmengen der komplexen Ebene definiert sind.
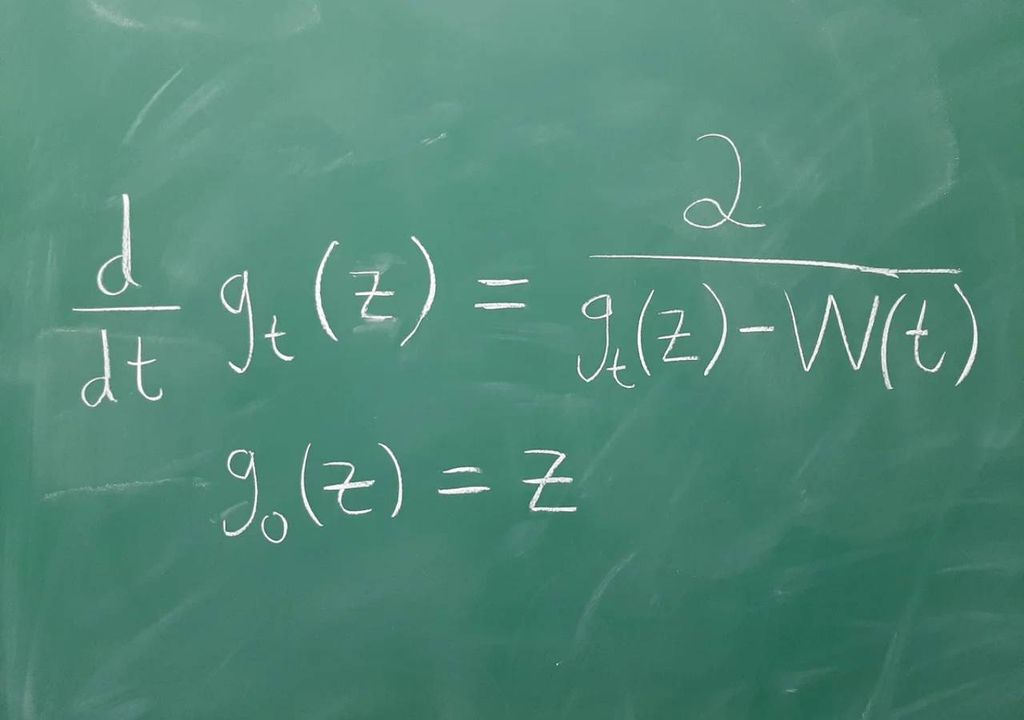
Fast 80 Jahre später, im Jahr 1999, entdeckte Oded Schramm, dass die Lösung der Loewner-Gleichung besondere Symmetrien aufweist, wenn die treibende Funktion als Brownsche Bewegung betrachtet wird, eine Zufallsfunktion, die ein zentraler Untersuchungsgegenstand der Wahrscheinlichkeitstheorie ist.
Auf der Grundlage von Schramms Entdeckung wurde gezeigt, dass die Lösung der Loewner-Gleichung für diese Wahl der Antriebsfunktion, die so genannte Schramm-Loewner-Evolution, das großräumige Verhalten mehrerer kritischer Modelle in der zweidimensionalen statistischen Mechanik beschreibt.
Laut Ewain Gwynne von der University of Chicago hat diese Gleichung die mathematische Untersuchung der statistischen Mechanik revolutioniert und zu einigen der interessantesten mathematischen Entdeckungen der letzten zwei Jahrzehnte geführt.
Gauß-Bonnet-Gleichung
Die Gauß-Bonnet-Formel ist eine schöne Gleichung in der Differentialgeometrie, die die Ungleichheit des Gaußschen Krümmungsintegrals über einer Fläche und einer Konstante multipliziert mit der Euler-Charakteristik der Fläche aufstellt.
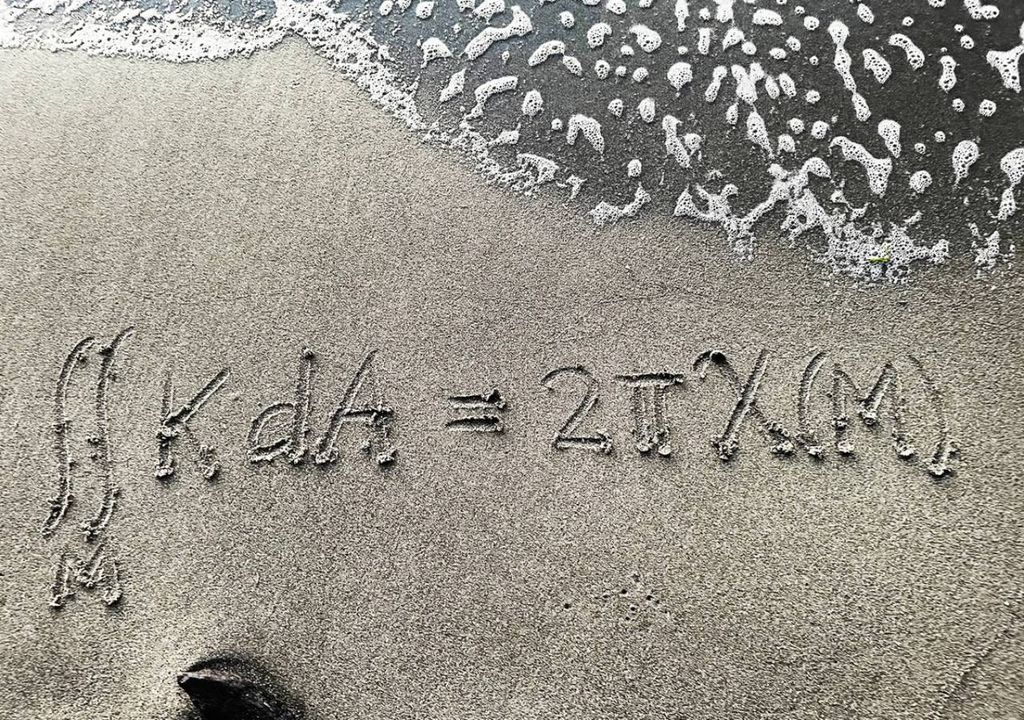
Die Gleichung zeichnet sich dadurch aus, dass sie zwei sehr unterschiedliche Größen miteinander in Beziehung setzt: die Krümmung der Oberfläche einerseits und die Topologie der Oberfläche andererseits.
Die Euler-Charakteristik ist eine globale topologische Invariante der Oberfläche, die die topologische Struktur der Oberfläche unabhängig von der Art ihrer Krümmung beschreibt.
Laut Ailana Fraser von der University of British Columbia sind einige der schönsten Aspekte dieser Gleichung die Einfachheit ihres Ausdrucks.
Eine unendliche Summe
Diese wichtige und anscheinend grundlegende Funktion, die mit dem Addieren und Zählen zu tun hat, ist schön und vielleicht unerwartet komplex.
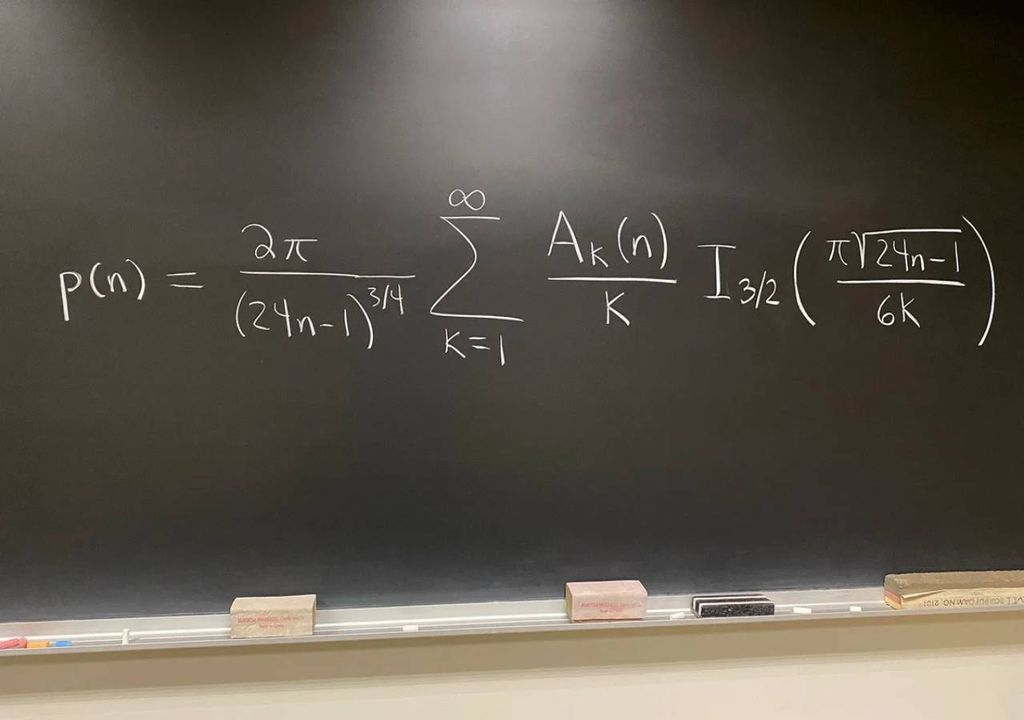
Die rechte Seite dieser Gleichung ist dank der Arbeit von Hans Rademacher aus dem Jahr 1937 eine exakte Formel.
Manche mögen die (große) rechte Seite, eine unendliche Summe, die u. a. Summen von (imaginären) komplexen Zahlen (Ak(n)), Bruchpotenzen (3/4 und die Quadratwurzel) und die transzendente Zahl Pi enthält, alsdas Gegenteil von schön oder als einschüchternd betrachten - zumal sie die (visuell kleine) linke Seite ersetzt, die sogar ein Kind verstehen kann.
Amanda Folsom vom Amherst College sagt, es sei schön, dass die hier gezeigte unendliche Summe konvergiert, was bedeutet, dass sie sich zu etwas Endlichem summiert, einer realen Zahl, die etwas Wichtiges aussagt, und dass sie sich nicht immer weiter summiert.




