Geometrie vs. Natur: So bilden natürliche Stoffe räumliche Strukturen aus – ganz anders als mathematische Modelle

Das Ausfüllen des Raums mit einfachen Strukturen ist ein zentrales Problem der Geometrie. Derweilen die klassische Geometrie oft auf scharfen Kanten und flachen Oberflächen basiert, zeigt die Natur eine klare Präferenz für weichere, gekrümmte Formen. Die Frage ist daher, wie man weiche natürliche Formen mittels scharfen Parkettierungen mathematisch beschreiben kann.

Eine neue Studie zeigt nun, dass man diese natürlichen Strukturen durch sogenannte weiche Parkettierungen nachbilden kann, da diese den Raum mit minimalen scharfen Ecken ausfüllen. Das britisch-ungarische Wissenschaftlerteam führte dafür eine neue Klasse von Formen ein: weiche Zellen, die nur wenige scharfe Ecken aufweisen und den Raum als weiche Kacheln ausfüllen.

Von scharfen Kanten zu weichen Zellen

Traditionell beschäftigt sich die Geometrie mit der lückenlosen Füllung von Räumen, sei es durch Dreiecke, Quadrate oder Polyeder. Die klassischen geometrischen Formen haben stets ebene Flächen und scharfe Ecken. In der Natur jedoch dominieren Strukturen mit gekrümmten Kanten und Oberflächen, die sich mathematisch vor allem durch weiche Parkettierungen und weiche Zellen modellieren lassen.

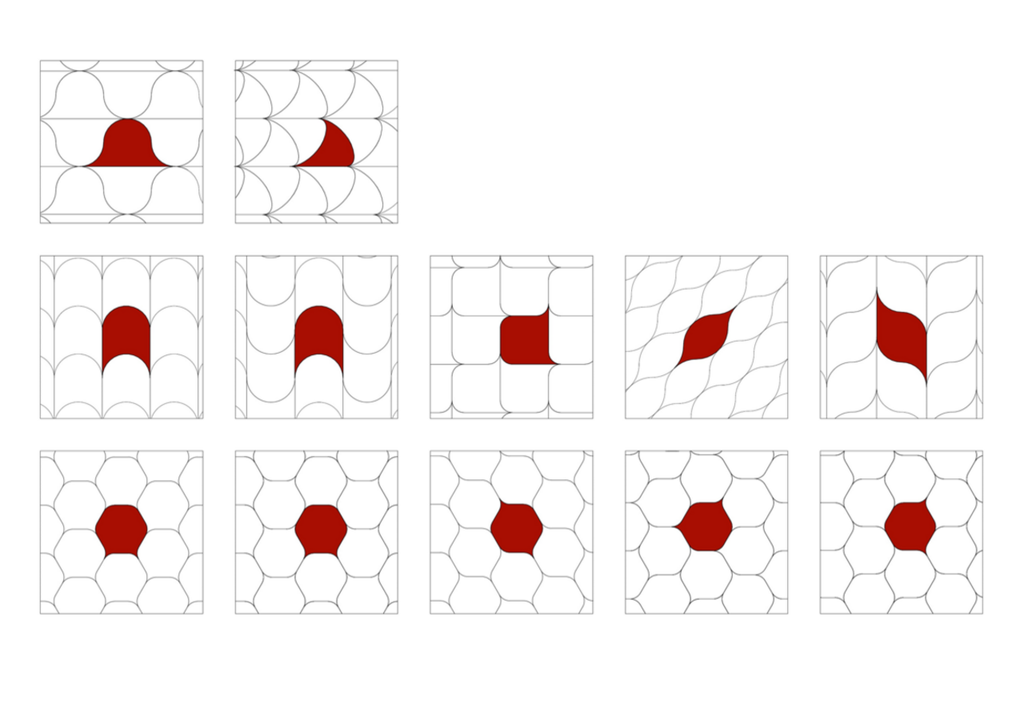
Solche weichen Zellen minimieren die scharfen Ecken und lassen sich dennoch nahtlos aneinanderfügen. Der entscheidende Unterschied zu klassischen Polyedern ist, dass die Kanten und Flächen nicht strikt gerade oder flach sind, sondern gekrümmt. So entstehen Strukturen, die flexibler und gleichzeitig effizient raumfüllend sind.

„Es ist bemerkenswert, dass diese idealen weichen Formen, die sich aus der Geometrie ergeben, reichlich in der Natur vorkommen, von Zellen bis zu Muscheln“, so Gábor Domokos, Professor für Morphologie an der Budapest University of Technology and Economics und Hauptautor der jüngst in Nature veröffentlichten Studie.

Der Ursprung der Parkettierungstheorie liegt in der Antike, bei den platonischen Körpern. Platon glaubte, dass lediglich fünf regelmäßige Polyeder den Raum lückenlos ausfüllen und unter anderem die vier Elemente Feuer, Wasser, Luft und Feuer oder sogar – im Falle des Dodekaeders – den gesamten Kosmos formten. Diese Vorstellung wurde später durch Aristoteles und moderne Mathematik widerlegt. Dennoch führten diese Überlegungen zur Entwicklung grundlegender geometrischer Werkzeuge wie des Raumwinkels.

Im 19. Jahrhundert untersuchte dann Lord Kelvin die optimale Füllung des Raums durch Schaumbläschen. Seine sogenannte Kelvin-Struktur wurde später durch die Weaire-Phelan-Struktur verbessert, die weniger Energie benötigt und die Oberflächenspannung optimiert. Die Schaumstrukturen sind ein Vorbild für die weichen Zellen der neuen Theorie.

Ein zentrales Konzept der Studie ist die kombinatorische Äquivalenz. Sie beschreibt, wie scheinbar unterschiedliche Strukturen durch elastische Verformung ineinander überführt werden können, ohne ihre grundlegenden Nachbarschaftsbeziehungen zu verlieren. Ein anschauliches Beispiel ist ein Gitter aus Gummi: Wird es verformt, ändern sich zwar die Form der Flächen und Kanten, aber die grundlegenden Verbindungen bleiben erhalten.

Demnach sind die weichen Zellen der Natur trotz ihrer gekrümmten Formen eng mit klassischen Polyedern verwandt. Sie sind jedoch flexibler und besser an physikalische Bedingungen wie Oberflächenspannung oder Elastizität angepasst. „Hier stellen wir eine neue Klasse von Mosaiken vor, die so genannten weichen Mosaike, bei denen die Zellen stark gekrümmte Flächen haben und die Anzahl der scharfen Ecken minimal ist“, erklärt Domokos.

Anwendungen und Beispiele

Die weichen Parkettierungen sind überall in der Natur zu finden: „Wir beweisen ein Theorem, das zeigt, dass weiche Kacheln im kombinatorischen Sinne in Fülle vorhanden sind, und wir zeigen, dass sich diese geometrischen Formen auffallend in natürlichen Beispielen widerspiegeln, die von biologischen Zellen bis zu den Kammern von Muscheln, einschließlich der Nautilus, reichen“, so Domokos.

Die Geometrie der Muschelkammern wird durch glatte, spiralförmige Grenzen definiert, die vor allem bei bestimmten Weichtieren, den Kopffüßern, zu finden sind, zu deren bekanntesten Beispielen die ausgestorbenen Ammoniten und der noch lebende Nautilus gehören, der für seine ikonische Spirale bekannt ist, die in Kammern unterteilt ist.

Das Tier lebt in der äußersten Kammer und nutzt eine Röhre, welche die Kammern miteinander verbindet, den sogenannten Siphuncle, um den Auftrieb zu kontrollieren. Das Gas-Flüssigkeits-Verhältnis wird in den Kammern angepasst, indem das Wasser aus den Kammern entfernt und durch Gas ersetzt wird, beim Nautilus hauptsächlich Stickstoff, Kohlendioxid und Argon. – Es existieren bereits geometrische Modelle, wie Seilachers Papier- und Ballonmodell, welche die Form der Kammerwände zu beschreiben versuchen.

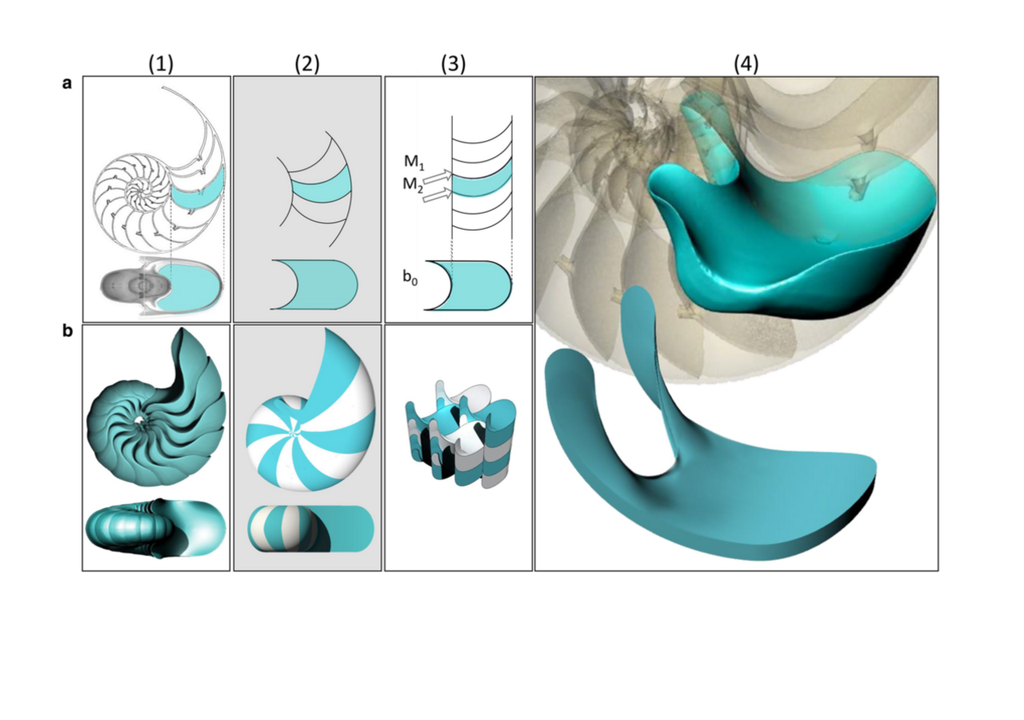
Zwei orthogonale Schnitte der Schale ermöglichten den Wissenschaftlern nun die Modellierung der 3D-Geometrie. Zunächst nahmen sie eine ideale Flachheit der Schale an (Spiralmodell), danach vereinfachten sie den Meridianschnitt zu einem geraden Prisma (prismatisches Modell).

Das 3D-Modell entstand dabei ebenfalls in zwei Schritten: Erst wurden parallele, zylindrische Flächen eingefügt, wodurch eine weiche Z-Zelle mit scharfen Ecken entstand. Anschließend glättete ein Kantenbiegealgorithmus die Zelle. Das Spiralmodell erzeugt ebenfalls raumfüllende Kacheln, umfasst jedoch unendlich kleine und große Zellen aufgrund der Spiralgeometrie.

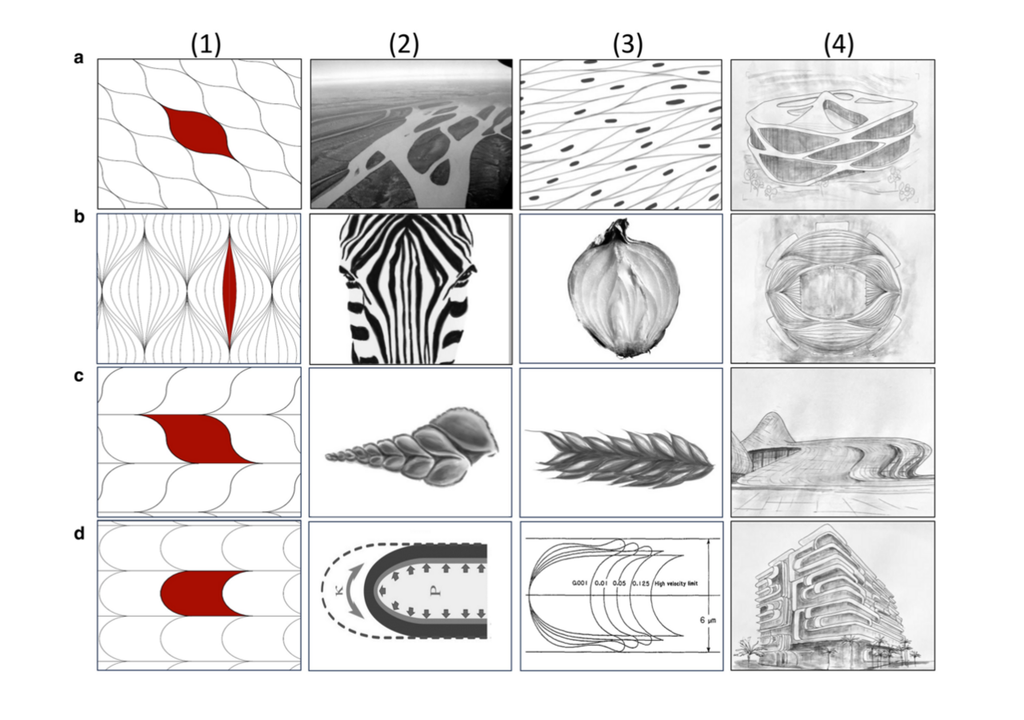
Auch in der Architektur finden sich solche Muster wieder. Die berühmte Architektin Zaha Hadid nutzte geschwungene Formen, die weichen Zellen ähneln, um futuristische Gebäude mit fließenden Übergängen zu schaffen. Die Künstler Katsushika Hokusai oder Victor Vasarely arbeiteten ebenfalls mit weichen 2D-Zellen.

Die Einführung der weichen Parkettierungen erweitert die klassische Geometrie grundlegend. Indem sie Formen mit großen Krümmungen und minimalen scharfen Ecken zulässt, eröffnet sie neue Wege für Design, Materialwissenschaften und biologische Modellierungen. Mit dem Kantenbiegealgorithmus lassen sich weiche Zellen aus klassischen Polyedern erzeugen. Die Methode könnte künftig dabei helfen, optimierte Materialien mit minimaler Oberflächenspannung zu entwickeln.

Die weichen Zellen und Parkettierungen zeigen, wie sich die Mathematik der Natur immer weiter annähert. Die Konzepte liefern damit einerseits ein besseres Verständnis der natürlichen Welt, andererseits auch neue Werkzeuge für Ingenieure, Architekten und Wissenschaftler.

Quellenhinweis:

Gábor Domokos, Alain Goriely, Ákos G. Horváth, Krisztina Regős (2024): Soft cells and the geometry of seashells, PNAS Nexus, 3, 9, pgae311. https://doi.org/10.1093/pnasnexus/pgae311