Die Mathematik des Hula-Hoops entschlüsselt: Darum schweben Reifen an manchen Körpern besser – und an anderen nicht

Hula-Hoop dürfte den meisten als Kinderspiel bekannt sein. US-amerikanische Wissenschaftler haben nun die Mathematik dahinter untersucht. In Laborexperimenten überprüften sie, welche Körperform am ehesten den Schwebezustand von Miniaturreifen aufrecht erhielt.

Hula-Hoop ist eine beliebte und gesunde Freizeitaktivität, die physikalisch betrachtet auch ein Beispiel für das freie Schweben ist, die sogenannte mechanische Levitation, die auf geometrischen Faktoren basiert. Nun haben erstmals Mathematiker den Hula-Hoop als physikalisches Phänomen detailliert untersucht.

Der Markenname Hula-Hoop stammt aus den 1950er Jahren, als ein US-amerikanischer Spielzeugfabrikant einen weltweiten Hype um den Kunststoffreifen auslöste. Der Name verbindet den hawaiianischen Tanz Hula mit dem englischen Begriff für Fassreifen (hoop).

Eine neue Studie des Courant Institute of Mathematical Sciences der New York University (NYU) wollte grundlegende Fragen beantworten: Wie bleibt der Reifen gegen die Schwerkraft in der Luft, und welche Rolle spielt dabei die Form des Körpers? Die Ergebnisse könnten künftig innovative Anwendungen in der Robotik und Energienutzung inspirieren.

Leif Ristroph, außerordentlicher Professor am Courant Institute und leitender Autor der in Proceedings of the National Academy of Sciences erschienenen Studie, erklärt: „Wir waren besonders daran interessiert, welche Arten von Körperbewegungen und -formen den Reifen erfolgreich in der Luft halten können.“ Dazu wurden im Applied Mathematics Laboratory der NYU Miniatur-Hula-Hoop-Experimente durchgeführt, bei denen 3D-gedruckte Roboterkörper in verschiedenen geometrischen Formen – beispielsweise Zylinder, Kegel oder Sanduhren – zum Einsatz kamen. Die Körper wurden von Motoren angetrieben und sollten die menschliche Bewegung simulieren.

Verschiedene Reifenformen — Bilder: Reifen auf verschiedenen Formen: zylindrischer Körper (A), (B und C) Kegel und (D) Hyperboloid. Schemata: (A) Ein rotationssymmetrischer Körper mit der Form RB(z) und deren Steigungswinkel β(z). Der Reifen-Mittelpunkt hat die Höhe z, σ ist der Neigungswinkel mit der Horizontalen. (B) Der Körper kreist um einen Kreis mit dem Radius RG, wobei θ = ωt die Bewegung des Körperzentrums bestimmt. Der Ring mit Radius RH und seine Lage in der Ebene wird durch den Winkel δ beschrieben. Bilder: Zhu, Pomerenk & Ristroph, 2025

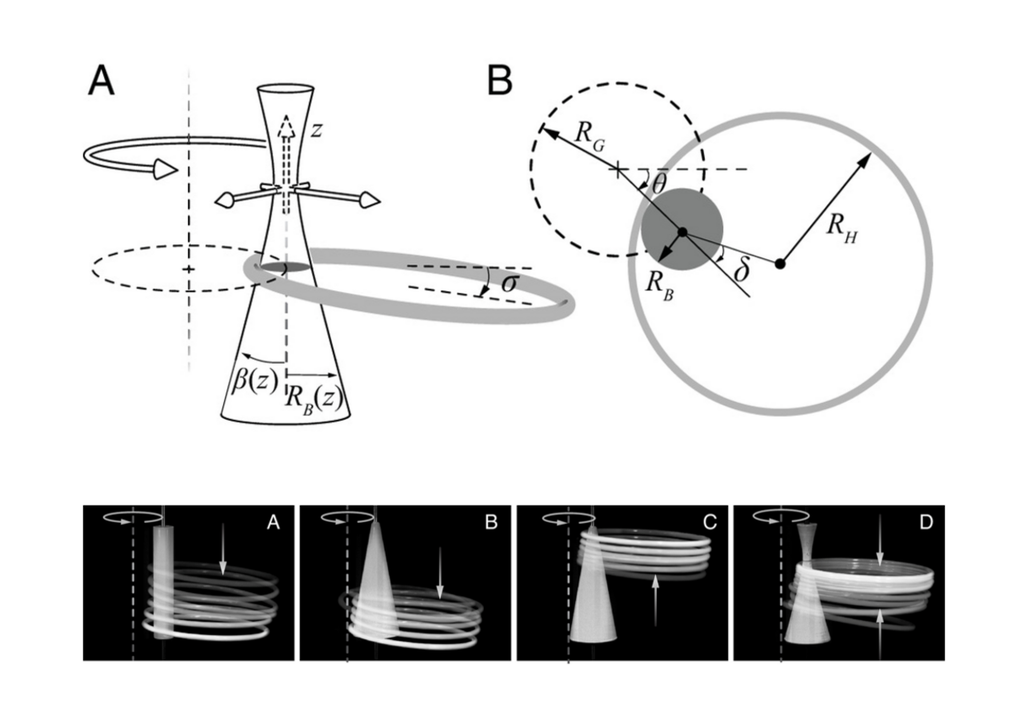
Hochgeschwindigkeitskameras zeichneten die Bewegungen der Miniaturreifen auf, die einen Durchmesser von 15 Zentimetern hatten. Die Experimente zeigten, dass die Bewegungsform oder der Querschnitt des Körpers, etwa Kreis oder Ellipse, keine entscheidende Rolle spielt. Stattdessen erwies sich die Körperform als ausschlaggebend, um den Reifen gegen die Schwerkraft in der Schwebe zu halten.

Die ideale Hula-Hoop-Form

Die Forscher identifizierten zwei zentrale Faktoren, die einen erfolgreichen Hula-Hoop-Durchgang ermöglichen: eine schräge Fläche („Hüfte“) zum Hochdrücken des Reifens und eine kurvige Form („Taille“), die den Reifen stabilisiert. „Menschen haben viele verschiedene Körpertypen – einige haben diese Neigung und Krümmung in Hüfte und Taille, andere nicht“, sagt Ristroph. Die Ergebnisse könnten erklären, warum manche Menschen von Natur aus den Hula-Hoop beherrschen, während andere sich eher schwer tun.

Die Experimente zeigten, dass diese spezifischen geometrischen Eigenschaften nicht nur für die Stabilität, sondern auch für die Dynamik des Reifens entscheidend sind.

Die Autoren entwickelten ein mathematisches Modell, das die komplexen Wechselwirkungen zwischen Reifenbewegung, Körperform und Kontaktkräften beschreibt. Die Formeln bieten einerseits Einblicke in die Dynamik des Hula-Hoops und könnten andererseits auch einen Weg in die praktische Anwendung finden. Ristroph zufolge könnte das Verständnis der Mechanik dabei helfen, Energie aus Vibrationen effizienter zu gewinnen oder die Bewegung und Positionierung von Robotern in der industriellen Fertigung zu verbessern.

Alltägliches neu betrachtet

„Wir waren überrascht, dass eine so beliebte, gesunde und unterhaltsame Aktivität wie Hula-Hoop nicht einmal auf grundlegender physikalischer Ebene verstanden wurde“, so Ristroph. Die Studie zeige, dass die Physik hinter dieser scheinbar simplen Aktivität sehr subtil ist und weitreichende Implikationen für Technik und Industrie haben kann.

Mit der Kombination aus Experimenten und mathematischer Modellierung wirft die Forschung ein neues Licht auf mechanische Systeme mit rollenden Kontaktpunkten – ein Prinzip, das in vielen technischen Anwendungen vorkommt. Die Ergebnisse könnten dazu beitragen, innovative Strategien zur Bewegungssteuerung zu entwickeln und die Energieeffizienz zu steigern.

Quellenhinweis:

Zhu, X., Pomerenk, O., & Ristroph, L. (2025): Geometrically modulated contact forces enable hula hoop levitation, Proceedings of the National Academy of Sciences, 122 (1) e2411588121. https://doi.org/10.1073/pnas.2411588121